O Indutor
Veja também:
Pequenos Negócios - Como Ganhar Dinheiro na Internet
O indutor é um componente muito utilizado em eletrônica. Podemos dizer que o indutor é um "primo" do Capacitor. O Capacitor funciona
armazenando energia no campo elétrico em seu interior. Já o Indutor funciona armazenando a energia no campo magnético. O Capacitor precisa
de tensão para armazenar energia. Já o indutor precisa de corrente para armazenar energia. Componentes como resistores, fios, transistores
etc funcionam transformando energia mas não armazenam energia. Os únicos componentes com esta propriedade são os Capacitores, os Indutores
e as pilhas e baterias.
Na figura 1 apresentamos as formas comerciais mais comuns para os indutores:
 Fig 1
Fig 1
O Indutor funciona por um princípio físico estudado por vários cientistas (Hans Christian Öersted, Ampère, Henry, Faraday,
Lenz, Neumann, Gauss e outros). Basicamente, sempre que uma corrente elétrica percorre um fio condutor ela induz um campo magnético H ao redor
deste fio. Este fenômeno está representado na figura 2.
 Fig 2
Fig 2
A direção das linhas de campo magnético é dada pela Regra da Mão Direita. Por esta regra, você aponta o
polegar de sua mão direita na direção da corrente e os outros dedos dão o sentido das linhas de campo.
Se no lugar de 1 fio, tivermos 2 ou mais fios em paralelo, a indução de campo magnético é a soma dos campos induzidos por cada fio.
Se agora nós enrolarmos o fio em espiral, conforme a figura 3, obteremos o componente conhecido como Indutor. Se você aplicar a Regra da Mão
Direita a cada seção do fio, concluirá que todas as linhas de campo no interior do indutor estão orientadas na mesma direção (figura 3).
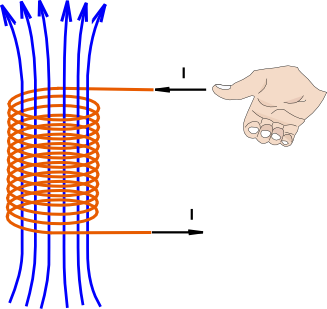 Fig 3
Fig 3
Para quantificar a intensidade do campo magnético foram criados alguns conceitos:
Força Magnetomotriz:
Se num Capacitor a Voltagem é a grandeza física que provoca o armazenamento de energia, no Indutor é a Força Magnetomotriz (F). F é dada por:
F = n . i; (fórmula 1)
onde n é o número de espiras do indutor e i é a corrente.
Campo Magnético H
Os físicos franceses Jean-Baptiste Biot e Félix Savart, estudaram a relação entre a corrente que circula pelo fio e o campo induzido ao
redor deste fio. Eles descobriram que se pegarmos qualquer caminho fechado em volta do fio e multiplicarmos a intensidade do campo magnético H,
num determinado ponto, pelo comprimento do caminho naquele ponto onde H pode ser considerado constante, e repetirmos para todo o caminho, o
resultado será a corrente total que atravessa este caminho.
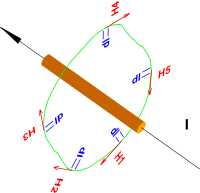 Fig 4
Fig 4
Para quem conhece o conceito de integral, o resultado é:
I = ∫ H. dl; (fórmula 2)
Para quem não conhece integral, a fórmula acima diz que: se você dividir o caminho (em verde) da figura 4 em segmentos bem pequenos, de mesmo
tamanho, medir a intensidade do campo H para cada segmento e multiplicar pelo tamanho do segmento, fazendo isso para todos os segmentos e
somando os resultados, no final você obterá o valor da corrente que passa dentro do caminho. Isto é muito importante, porque permite calcular
a intensidade do campo a uma certa distância do fio.
Quando construímos um indutor, conforme a figura 3, o campo H no interior do indutor pode ser calculado por uma variação da fórmula 2:
n . i = ∫ H. dl; (fórmula 3)
Onde n é o número de espiras e i a corrente que passa pelo indutor.
Logo:
F = ∫ H. dl; (fórmula 4)
Ou seja, a intensidade do Campo H no interior do Indutor é diretamente proporcional à
Força Magnetomotriz.
Campo Induzido B
O Campo H se relaciona com outra grandeza chamada de Campo Induzido (B),
da seguinte forma:
B = µ . H; (fórmula 5)
O fator µ é chamado de permeabilidade magnética do material e depende do material por onde as linhas de campo H estão passando.
Pela fórmula 5 nós vimos que quando temos um campo H, temos também um Campo Induzido B, que depende do material por onde o campo H passa.
Os materiais Ferromagnéticos tem a propriedade de intensificar o Campo Magnético induzido B. Se nós montarmos o
indutor com um núcleo de material ferromagnético, conforme a figura 5, o campo H será o mesmo, se mantivermos a corrente e o número de espiras.
Mas o Campo Induzido B dependerá da permeabilidade magnética µ do núcleo . A Permeabilidade Magnética de um material é dada por:
µ = µr . µo; (fórmula 6)
Onde: µr é a permeabilidade relativa do material e µo é a permeabilidade magnética do vácuo.
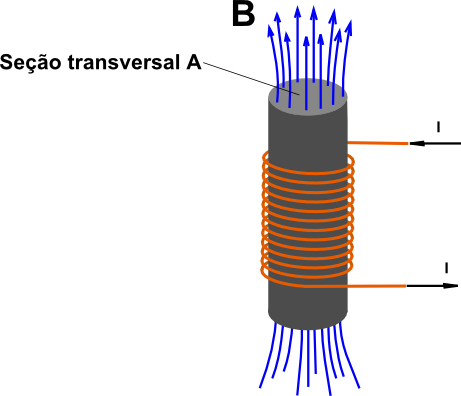 Fig 5
Fig 5
Concluímos então que se escolhermos um núcleo com µr > 1, nós intensificaremos o Campo B se comparado com um Indutor com
núcleo de ar (µr do ar = 1). Alguns materiais tem µr bem elevado. A seguir alguns deles:
- ferro: µr = de 200 a 600;
- níquel: µr = 100;
- permaloy: µr = 8000;
- mumetal: µr = 20000;
Fluxo Magnético Ø
Vamos considerar que a intensidade do Campo Magnético B no interior do Indutor da figura 5 seja relativamente constante em toda a seção reta
do núcleo (A). Isto é verdade se o comprimento do indutor for muito maior que o diâmetro e se o núcleo apresentar um
µr elevado. Se agora multiplicarmos a intensidade do Campo B pela área A da seção transversal, obteremos o valor da
grandeza denominada de Fluxo Magnético Ø. A energia de um indutor é armazenada neste
Fluxo Magnético. Matematicamente temos:
Ø = B . A; (fórmula 7)
Relutância ℜ
O conceito de Relutância (ℜ) foi criado para relacionar o Fluxo Ø com a Força Magnetomotriz F. Esta relação é dada por:
F = ℜ . Ø; (fórmula 8)
Note a semelhança da fórmula 8 com a Lei de Ohm que relaciona Voltagem e Corrente ( V = I . R ). F, ℜ e Ø são os equivalentes,
nos circuitos magnéticos, de V, R e I dos circuitos elétricos. E de fato, para cálculos de circuitos magnéticos esta equivalência é utilizada
constantemente.
Se analisarmos as fórmulas de circuitos magnéticos apresentadas acima, é fácil concluir que a Relutância de um material é dada por:
ℜ = 1 / ( µ . A ); (fórmula 9)
Indutância L
Finalmente podemos definir a grandeza mais importante para um Indutor: a Indutância.
No Capacitor a Capacitância relaciona a Voltagem com a Carga Elétrica acumulada. Já, no Indutor, a Indutância relaciona a corrente com o
Fluxo Ø, da seguinte forma:
L = (n . Ø) / I; (fórmula 10)
Onde n é o número de espiras, I é a corrente e Ø o Fluxo.