M016 - Leis de Kirchhoff

Veja também:

Pequenos Negócios - Como Ganhar Dinheiro na Internet

Leis de Kirchhoff

Nós ja estudamos as Leis de Ohm e as Leis de Joule. Neste Módulo e no próximo estudaremos as Leis de Kirchhoff, que em conjunto com as anteriores, compõem o grupo de leis básicas da eletrônica.

Para entendermos as Leis de Kirchhoff, inicialmente temos que definir o que é Nó, Malha e Ramo. Para isto, observe o circuito da figura 1.

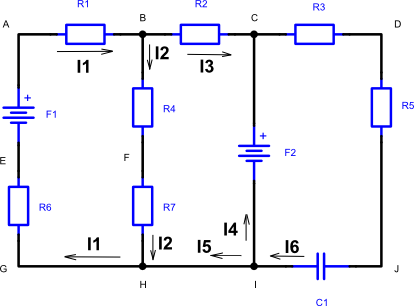Fig 1

Nó: é um ponto do circuito onde 3 ou mais condutores são ligados.
Malha: é qualquer caminho fechado do circuito, ou seja, é qualquer caminho que volta ao ponto inicial.
Ramo: é o caminho aberto entre dois nós. O Ramo se inicia em um Nó, termina em outro Nó e não contém nenhum Nó entre estes dois.

Na figura 1:

B, C, H e I são exemplos de Nós;

A, D, E, F, G e J não são Nós;

O caminho A-B-F-H-G-E-A é exemplo de Malha;

O caminho A-B-C-I-H-G-E-A é outro exemplo de Malha;

O caminho B-F-H é um exemplo de Ramo;

Mas

O caminho B-C-I não é exemplo de Ramo, já que tem outro Nó entre B e I.

Primeira Lei de Kirchhoff ou Lei dos Nós

"A soma das correntes que entram em um nó é igual a soma das correntes que deixam o nó."

Ainda utilizando o circuito da figura 1, a Primeira Lei de Kirchhoff, diz que:

Para o Nó B: I₁ = I₂ + I₃

E ainda para o Nó I: I₆ = I₄ + I₅

Nem sempre você sabe qual a direção da corrente que está entrando (ou saindo) de um Nó. Por isso precisamos adotar uma convenção. A corrente que está entrando em um Nó tem sinal positivo. A corrente que está saindo de um Nó tem sinal negativo. Assim, se seus cálculos indicarem que uma corrente é negativa, ela está saindo do Nó. Se der positivo ela está entrando no Nó.

No exemplo da figura 1, se I₁ = 2A e I₂ = -1A(saindo do Nó), então I₃ = -1A (saindo do Nó).

Esta definição da Lei de Kirchhoff, enunciada acima, pode ser colocada de uma forma matemática mais completa que é a seguinte:

"A soma das correntes que entram e saem de um Nó é igual a zero."

Para isto, o sinal de cada corrente tem de ser considerado.

Para o Nó I ficaria assim: I₄ + I₅ + I₆ = 0;

Segunda Lei de Kirchhoff ou Lei das Malhas

"A soma das diferenças de potencial em uma malha é igual a zero."

Ainda utilizando o circuito da figura 1, a Segunda Lei de Kirchhoff, diz que:

Para o Malha A-B-F-H-G-E-A:

V_AB + V_BF + V_FH + V_GE + V_EA = 0 ;

Se a fórmula acima ficou confusa, recorde aqui o conceito de Diferença de Potencial (ddp).

Aqui também temos que adotar uma convenção para o sinal da diferença de potencial (ddp). Considere o sinal da ddp positivo se a corrente estiver entrando pela primeira conexão do componente (em V_AB, A é a primeira conexão e B a segunda). Na figura 1 você deve ter observado que as correntes I₁ e I₂ aparecem 2 vezes. Isto acontece porque, como consequência da Primeira Lei de Kirchhoff, a corrente que entra em um Ramo do circuito é a mesma que sai deste Ramo.

OK. Então aplicando a Segunda Lei de Kirchhoff, já sabemos que para a Malha A-B-F-H-G-E-A vale V_AB + V_BF + V_FH + V_GE + V_EA = 0. Se considerarmos que os sentidos das correntes indidados na figura 1 estão corretos, os sinais da ddps serão os seguintes:

V_AB positivo;

V_BF positivo;

V_FH positivo;

V_GE positivo;

V_EA positivo;

Mas veja que inicialmente você não sabe o sentido das correntes. Assim, ao calcular o circuito, inicialmente você precisa calcular cada corrente de cada Ramo e só depois aplicar a Segunda Lei de Kirchhoff.

Para a mesma Malha citada acima, a Segunda Lei de Kirchhoff poderia ser aplicada da seguinte forma:

V_AE + V_EG + V_HF + V_FB + V_BA = 0 ;

Mas neste caso, observe que a corrente entra pelo contato oposto considerado na ddp (em V_BA, por exemplo, a corrente entra por A, que é o segundo contato considerado na ddp).

Assim o sinal das ddps ficariam:

V_AE negativo;

V_EG negativo;

V_HF negativo;

V_FB negativo;

V_BA negativo;