M019 - Exercícios de Eletrônica
Índice Geral do Curso de Eletrônica
Como Ganhar Dinheiro com Eletrônica
Exercícios 1 - Respostas
Neste Módulo as respostas para os exercícios do Módulo anterior.
No circuito da figura 1, sabemos que:
- F1 = 12V;
- R1 = 10R;
- R2 = 20R;
- R3 = 40R;
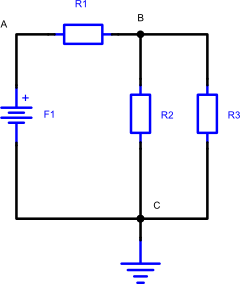 Fig 1
Fig 1
1) Calcule o valor da tensão nos seguintes pontos:
A, B e C.
Resposta:
A tensão VA = VF1 = 12V.
Para calcularmos a tensão VB no ponto B,primeiro nós vamos calcular o resistor
RP, equivalente ao paralelo de R2 e R3.
RP = (R2 x R3) / (R2 + R3) = (20 x 40) / (20 + 40) = 13,3 ohms.
Agora vamos calcular o resistor RS, equivalente à série de R1 e RP,
calculado acima.
RS = R1 + RP = 10 + 13,3 = 23,3 ohms.
Agora podemos calcular a corrente total fornecida por F1:
IF1 = VF1 / RS = 12 / 23,3 = 0,515A.
O valor da tensão no ponto B será a tensão fornecida por F1 - a ddp em R1:
VR1 = IF1 x R1 = 0,515 x 10 = 5,15V.
Logo:
VB = VF1 - VR1 = 12 - 5,15V = 6,85V.
A tensão no ponto C é 0V, ja que é nossa referência GND.
2) Calcule a corrente fornecida pela Fonte F1.
Resposta:
Nos calculos anteriores já encontramos IF1 = 0,515A ou, se preferir, 515mA (miliaperes).
3) Calcule a potência mínima para o resistor R1.
Resposta:
Pelas formulas de potência de Joule, a potência dissipada por R1 é dada por:
PR1 = (VR1)2 / R1 = 5,152 / 10 = 2,65W.
Logo temos que escolher um resistor com potência de dissipação superior a 2,65W. Podemos escolher um resistor de
10R 3W que é comercial.
No circuito da figura 2 sabemos que:
- F1 = 24V;
- R1 = 10R;
- R2 = 20R;
- R3 = 10R;
- R4 = 10R;
- R5 = 20R;
- R6 = 2R;
- R7 = 10R;
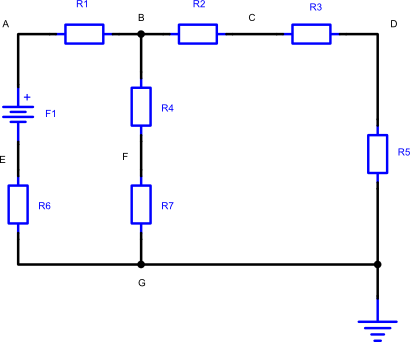 Fig 2
Fig 2
4) Calcule o valor da tensão nos seguintes pontos:
A, B, C, D e F. Dica: calcule a associação série RS1 de R2, R3 e R5. Depois
calcule a associação em série RS2 de R4 e R7. Ai calcule a associação em paralelo
RP1 destes valores calculados por você (RS1 e RS2). O circuito ficará bem simples,
permitindo aplicar a Lei de Ohm e a Lei de Kirchhoff. Mas vai dar trabalho!!
Resposta:
Apesar de trabalhoso, este exercício segue uma solução semelhante ao anterior.
Primeiro vamos calcular a série RS1 de R2, R3 e R5:
RS1 = R2 + R3 + R5 = 50 ohms.
Agora vamos calcular RS2 equivalente a série de R4 e R7:
RS2 = R4 + R7 = 20 ohms.
Agora vamos calcular o resistor RP1 equivalente ao paralelo de RS1 e RS2
RP1 = (RS1 x RS2) / (RS1 + RS2) = (50 x 20) /(50 + 20) = 14,3 ohms.
Depois de todas estas substituições pelos equivalentes série e paralelo, o circuito da figura 2 ficou como o da figura 2b abaixo:
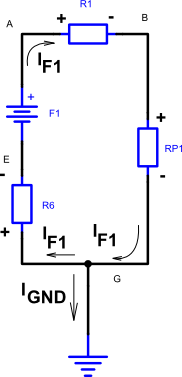 Fig 2b
Fig 2b
No circuito equivalente da figura 2b, a corrente IGND é zero, pois só temos uma referência GND no circuito e ela
não acumula carga. Assim, pela Lei dos Nós de Kirchhoff, podemos concluir qua a única corrente que circula na malha é IF1.
Pela Lei das Malhas de Kirchhoff, sabemos que a soma das ddps na malha fechada tem de ser igual a zero. Aqui é importante
observar a polaridade das ddps. Para cargas (todo componente que não gera corrente) o polo positivo da ddp é aquele por onde
entra a corrente. Já nas fontes, como sabemos, o polo positivo é aquele por onde sai a corrente. Assim se somarmos as ddps no
sentido horário, apartir do ponto A temos:
-VAB - VBG - VGE + VF1 = 0.
Logo:
VF1 = +VAB + VBG + VGE.
Que é igual:
VF1 = IF1x R1 + IF1x RP1 + IF1x R6.
Assim podemos calcular IF1 como:
IF1 = VF1 / (R1 + RP1 + R6) = 0,913A.
Assim a tensão no ponto A será dada por:
VA = - VGE + VF1 = - IF1 x R6 + 24V = 22,2V
Ai fica fácil calcular a tensão em B. Vamos fazer de duas formas diferentes e o valor tem que ser igual:
VB = VA - VAB = VA - IF1 x R1 = 22,2 - 9,13 = 13,1V
Ou, calculando de outra forma:
VB = IF1 x RP1 = 0,913 x 14,3 = 13,1V
Quando você fizer as contas na calculadora perceberá uma pequena diferença mas é em função dos arredondamentos adotados.
5) Calcule a corrente fornecida pela Fonte F1.
Resposta:
Como vimos no cálculo anterior IF1 = 0,913A ou, se preferir, 913 mA.
6) Calcule tensão no polo negativo da fonte F1.
Resposta:
VE = -IF1 x R6 = -0,913 x 2 = -1,83V
7) Calcule a ddp em R2.
Resposta:
Voltando ao circuito original da figura 2, já sabemos que VB = 13,1V. Assim a corrente IR2, que circula
pelo ramo formado por R2 + R3 + R5 é dada por:
IR2 = VB / RS1 = 13,1 / 50 = 0,262A.
Então a ddp VR2 em R2 vale:
VR2 = 0,262 x 20 = 5,24V.
No circuito da figura 3 sabemos que:
- F1 = 24V;
- F2 = 12V;
- R1 = 10R;
- R2 = 20R;
- R3 = 10R;
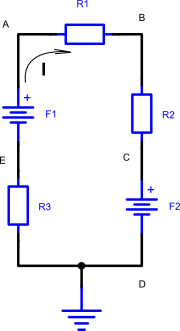 Fig 3
Fig 3
8) Calcule a corrente fornecida pela Fonte F1.
Resposta:
Este circuito é semelhante ao da figura 2b e já sabemos que a corrente I que circula pela malha é a mesma para todos os componentes.
Aplicando Kirchhoff, a partir de A e no sentido horário, temos:
- VAB - VBC - VF2 - VDE + VF1 = 0.
Logo:
VF1- VF2 = VAB + VBC + VDE.
Assim podemos calcular I como:
I = VF1- VF2 / R1 + R2 + R3 = 0,3A ou 300mA.
Observe que se a tensão de F2 fosse superior à de F1, I seria negativa, ou seja, ela estaria entrando no polo positivo de F1.
9) Calcule a corrente fornecida pela Fonte F2. Lembre-se
que, pelo sentido convencional da corrente, ela é positiva se sai do polo positivo da fonte.
Resposta:
A corrente fornecida por F2 = -I = - 300mA, já que está entrando no polo positivo da fonte.
10) Sabendo que tanto F1 quanto F2 são baterias recarregáveis,
F1 está se carregando ou se descarregando? E F2?
Resposta:
Como a corrente na saída de F1 é positiva, ela esta se descarregando. Já no caso de F2 a corrente é negativa. Então
F2 está se carregando.
Aqui temos que fazer uma observação importante. F2 neste último exercício está funcionando como carga pois não
está fornecendo potência para o resto do circuito. F2 está consumindo potência, ou seja, apesar de ser uma fonte está atuando como
uma carga.

