M020 - Campo Elétrico e Rigidez Dielétrica

Campo Elétrico e Rigidez Dielétrica

Nos Módulos anteriores deste curso, nós já estudamos o Resistor, que basicamente introduz uma resistência à passagem da corrente elétrica. O próximo componente eletrônico que nós vamos estudar é o Capacitor, mas para isto nós precisamos estudar o que é Campo Elétrico.

Quando você estuda física, você aprende que existem dois tipos de força de interação: a de contato e a de campo. A força de contato é aquela que ocorre entre dois corpos quando eles entram em contato, um com outro. Quando você está empurrando um carro, basicamente você está exercendo uma força de contato sobre o carro. Já a força de campo é uma interação entre partículas que ocorre à distância, sem o contato físico entre estas partículas. A força gravitacional é um exemplo de força de campo.

Na eletrônica, dois tipos de campos são de grande importância: O Campo Elétrico e o Campo Magnético.

Quando estes dois campos estão juntos você tem os campos eletromagnéticos, como, por exemplo, as ondas de rádio.

Neste Módulo vamos estudar o Campo Elétrico.

O Campo Elétrico

Nós já vimos em Módulos anteriores que a corrente elétrica é formada por cargas elétricas em movimento. Já vimos que o elétron é uma carga negativa e que o ion é uma carga positiva. Já vimos também que cargas elétricas de sinais opostos se atraem e de mesmo sinal se repelem.

Quem primeiramente estudou o fenômeno da interação entre cargas elétricas foi o físico francês Charles Augustin de Coulomb.

A interação entre as partículas elétricas se dá pela presença do campo elétrico. Cada partícula eletricamente carregada, tem associado a si um campo de força, chamado de campo elétrico, que atua sobre outras partículas eletricamente carregadas, que por ventura estejam nas proximidades da primeira carga. Esta interação aparece na forma de uma força de atração ou repulsão.

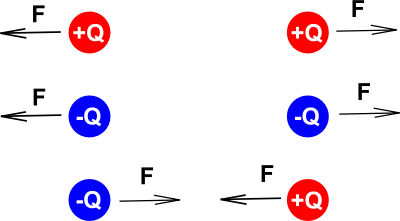Fig 1

Carregar um corpo com carga, significa desequilibrar as cargas positivas e negativas existentes neste corpo. Quando você tira uma blusa de lã (no tempo seco), é bem comum você perceber pequenas faíscas. Estas faíscas são causadas pela eletricidade estática da blusa e de seu corpo. Ao se movimentar, ainda vestido com a blusa, o atrito de sua pele com a blusa, arranca elétrons que vão desequilibrar a carga inicialmente nula de seu corpo e da blusa. Eles se carregam com cargas de sinais opostos. Assim, ao retirar a blusa, as faíscas são os elétrons pulando entre a blusa e seu corpo, tentando neutralizar novamente a carga total.

As forças de interação elétrica que aparecem quando a carga se encontra dentro de um Campo Elétrico, é uma Grandeza Vetorial, ou seja, além da intensidade, a direção de atuação também é importante.

Coulomb não só estudou como estas cargas interagem, como também quantificou quantidades de carga. Por este motivo, e em homenagem a ele, a unidade de carga elétrica e o Coulomb. Por exemplo, se um corpo está carregado com 2C (dois coulombs), ele tem o dobro de carga de um outro corpo carregado com 1C.

O Coulomb é uma unidade muito grande e corresponde à carga de todos elétrons que passam por um condutor, em 1 segundo, para uma corrente de 1A . Por ser uma unidade muito grande, normalmente a unidade utilizada em eletrônica é o microcoulomb - uC(1C / 1.000.000) ou o nanocoulomb - nC( 1C/1.000.000.000)

A força elétrica entre duas partículas, pode ser também muito elevada. Dois corpos carregados com 1C e colocados a 1 metro, um do outro, exercem uma força elétrica da ordem de 900.000 toneladas!

Voltando ao Campo Elétrico, então sempre que tivermos uma Carga Elétrica teremos também um Campo Elétrico. O Campo Elétrico, assim como a Força Elétrica, é uma Grandeza Vetorial, ou seja, além da intensidade tem também direção.

A intensidade de Campo Elétrico está intimamente ligada à voltagem de circuitos. Imagine a montagem da figura 2, onde conectamos uma fonte de tensão a duas placas condutoras paralelas.

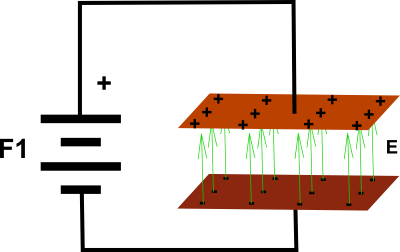Fig 2

Nesta montagem vai aparecer um Campo Elétrico, que por convenção, parte da carga negativa para a positiva. São os vetores E da figura 2. A intensidade de Campo Elétrico é medida em Volts por metro (V/m). Assim, se na figura 2 a tensão da fonte F₁ for de 1V e a distância entre as placas for de 1m, a intensidade do campo será de 1V/m.

Rigidez Dielétrica

Rigidez Dielétrica é a capacidade apresentada por um material isolante de se opor à passagem de corrente elétrica, quando submetido a um Campo Elétrico.

Na montagem da figura 2, entre as placas nós temos ar. Se começarmos a subir a tensão da fonte F₁, vai chegar um momento em que a força do campo elétrico sobre as moléculas que compõem o ar será tão grande que arrancará os elétrons destas moléculas em direção à placa positiva e os íons (átomos que perderam elétrons) em direção à placa negativa. Ocorrerá uma grande faísca de forma semelhante aos relâmpagos.

Esta intensidade mínima para iniciar este processo de condução intensa de corrente é chamado de Rigidez Dielétrica do material. Se no meio das placas montarmos qualquer outro material isolante, formando um sanduíche, poderemos encontrar a Rigidez dielétrica deste material, de forma semelhante ao exemplo do ar.

A seguir a Rigidez Dielétrica de alguns materiais:

Ar 3 x 10⁶ V/m
Baquelite 24 x 10⁶ V/m
Borracha de Neopreno 12 x 10⁶ V/m
Nylon 14 x 10⁶ V/m
Papel 16 x 10⁶ V/m
Polistireno 24 x 10⁶ V/m
Vidro Pyrex 14 x 10⁶ V/m
Quartzo 8 x 10⁶ V/m
Óleo de Silicone 15 x 10⁶ V/m
Titanato de Estrôncio 8 x 10⁶ V/m
Teflon 60 x 10⁶ V/m

A seguir um exemplo de aplicação do conceito de Rigidez Dielétrica:

1) Um dos materiais mais utilizados na fabricação de placas de circuito impresso é o fenolite. Sabendo que a espessura do fenolite é de 1,6mm e que a rigidez dielétrica deste material é de 15KV/mm (quinze kilivolts por milímetro), qual a máxima tensão pode ser aplicada em duas trilhas paralelas, uma em cada face da placa?

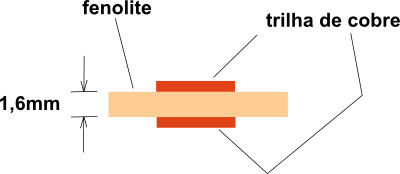Fig 3

Resposta:

A Rigidez informada de 15 KV/mm significa que o fenolite resiste a 15.000 volts para cada mm de espessura. Assim, sabendo que a espessura da placa é de 1,6mm, basta fazer a seguinte regra de 3:

1mm -> 15.000V

1,6mm -> X

Que resolvendo:

X x 1 = 1,6 x 15.000 Logo: X = 1,6 x 15.000 = 24.000V.

Então, por estes dados, você pode aplicar uma diferença de potencial de até 24.000V nas trilhas opostas desta placa de circuito impresso.