M036 - Cálculo de Fonte de Meia Onda
Índice Geral do Curso de Eletrônica
Veja também:
Pequenos Negócios - Como Ganhar Dinheiro na Internet
Cálculo de uma Fonte Linear com Retificação em Meia Onda
No Módulo anterior vimos os conceitos básicos das fontes com retificação em meia onda. Agora vamos mostrar
como realizar um projeto simples deste tipo de fonte.
O circuito que analisaremos é o mesmo do Módulo anterior:
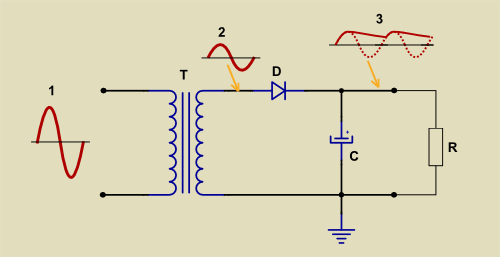 Fig 1
Fig 1
Para podermos analisar o comportamento da fonte da figura 1, primeiro precisamos entender como se comporta
um capacitor durante sua carga e descarga.
Observe o circuito da figura 2 abaixo:
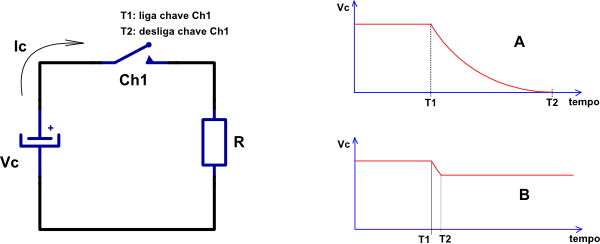 Fig 2
Fig 2
Vamos considerar 2 situações:
Na primeira a chave Ch1 é fechada em T1 e o capacitor se descarrega completamente até T2, conforme gráfico A.
Na segunda condição Ch1 é fechada em T1 e logo depois volta a ser aberta em T2, como no gráfico B.
No gráfico A da para ver claramente que a curva de descarga não é linear. Isto acontece porque a corrente de descarga
não é constante e vai caindo à medida que o capacitor descarrega.
Já no gráfico B, como o tempo de descarga é pequeno, dá para considerar a curva de descarga como uma reta. Isto porque
neste curto intervalo de descarga, a corrente Ic é praticamente constante.
De uma forma geral, a variação de tensão no capacitor para uma corrente de descarga constante Ic é dada pela
seguinte fórmula:
Δ Vc = (Ic x Δ T) / C (fórmula1)
Onde C é a capacitância do capacitor
Vejamos um exemplo de aplicação da fórmula 1 acima:
No circuito da figura 2, calcule a variação da tensão no capacitor, considerando
que a tensão de carga inicial Vc = 10V, a chave CH1 é ligada em T1 = 100mS e desligada em T2 = 116,6 mS. Sabemos
ainda que a capacitância do capacitor é de 4700uF e R = 1Kohms. Vamos considerar que a corrente de descarga é
praticamente constante durante este curto período de descarga.
Resposta:
A corrente Ic de descarga é dada por:
Ic = Vc / R então Ic = 10V / 1Kohms logo Ic = 10mA
ΔT = T2 - T1 = 16,6 mS
Lembre-se que para aplicar qualquer fórmula, todas as variáveis devem estar no mesmo sistema de unidades.
Convertendo para o Sistema Internacional temos:
Ic = 10mA = 0,01A
ΔT = 16,6mS = 0,0166 S
C = 4700uF = 0,0047F
Aplicando estes valores na fórmula 1 temos:
ΔVc = (0,01A x 0,0166) / 0,0047 logo ΔVc = 0,0353V = 35,3 mV
No exemplo acima, nós concluimos que se você ligar em paralelo com um capacitor de 4700uF carregado inicialmente com 10V,
um resistor de 1Kohms, por um período de 16,6mS, a variação de tensão no capacitor será de 35mV. Este cálculo será útil mais adiante.
Voltemos ao circuito da figura 1. Vamos analisar o funcionamento do circuito através de outro exemplo:
No circuito da figura 1, calcule a tensão eficaz de saída Ve, sabendo que a tensão de
entrada da rede é de 127Vac, a relação de transformação de T é de 10:1, a capacitância do capacitor é de 2200uF e a carga R é
de 100R. Considere a tensão de condução do diodo D como sendo 0,7V.
Resposta:
A resposta é longa, mas vai ajudar a entender o funcionamento da fonte.
Primeiro precisamos calcular a tensão de pico na entrada de nosso circuito. Como já vimos em
M032, a tensão de pico é dada por
Vrms x √2.
Como em nosso circuito a tensão rms de entrada é de 127Vac, a tensão de pico é dada por:
Vpe = 127 x 1.4142 = 179,6V
Onde Vpe é a tensão de pico na entrada do transformador T.
A relação de transformação foi dada como 10:1. Assim a tensão de pico na saída do transformador é dada por:
Vps = Vpe x 1 / 10 = 17,96V
Onde Vps é a tensão de pico na saída do transformador.
Pela figura 1 fica claro que esta tensão Vps é o valor máximo de carga do capacitor, durante o ciclo positivo
da tensão na saída do transformador. Mas como o diodo D tem uma tensão de condução informada de 0,7 V, temos que
descontar esta tensão. Assim:
Vcmax = 17,96 - 0,7 = 17,26V
Então já sabemos que para uma entrada de 127Vac, a tensão máxima no capacitor será de 17,26V.
Para continuarmos nossa análise, o circuito de saída de nossa fonte, formado pelo capacitor e a carga R
é semelhante ao circuito da figura 2, e o diodo funciona como chave Ch1, mas só que invertido. Enquanto D
está conduzindo, a tensão Vc é igual a tensão de saída do transformador - 0,7V de queda no diodo. Quando Vc
chega ao valor máximo e a partir deste instante, o diodo corta, é como estar no instante T1 da figura 2, onde o
capacitor passará a se descarregar via a carga R.
Podemos então calcular a tensão VR de ripple do circuito da mesma forma que calculamos ΔVc na figura 2.
Para isto podemos fazer as seguintes aproximações:
ΔT = 1/60 = 16,6mS (um ciclo de onda de 60Hz).
Ic = 17,26V / 100ohms = 0,172A
Assim:
VR = (0,172 x 0,0166) / 0,0022 logo VR = 1,28V
Pronto. Já sabemos que a tensão de ripple de nossa fonte é aproximadamente 1,28V. Estes cálculos são aproximados mas
funcionam muito bem se esta tensão de ripple for menor que 10% da tensão de carga do capacitor.
A tensão eficaz Ve pode ser facilmente cálculada como a média da tensão de saída:
Ve = (Vc + (Vc - VR)) / 2
logo:
Ve = (17,26V + (17,26V - 1,28V))/2 = 16,62V
Com estes cálculos conseguimos utilizar os conceitos principais envolvidos no projeto de fontes retificadoras
de meia onda. Vamos lançar agora o seguinte desafio:
Projete uma fonte retificadora em meia onda para uma tensão de saída de 12V. O
circuito que será alimentado com esta fonte consome 1A em 12V. Para que ele funcione adequadamente, a máxima tensão de
ripple permitida é de 1V. A tensão de entrada da fonte é de 220Vac. Calcule a relação de transformação do transformador e a
capacitância do Capacitor. Considere a tensão de condução do diodo de 0,7V.
Uma dica! Você precisará calcular a fonte de trás para frente! Começe pelo circuito de saída!
Depois mande seus cálculos para projetos@eletronpi.com.br que corrigimos para você!!!

